Hash Table

What is Hash Table
- Core Concepts
- Common operations of hash table
Hash Collision
- Separate Chaining
- Open Addressing
Hash Alogrithm
- Goals of hash algorithms
- Common hash algorithms
Practical Examples
- four sum

What is Hash Table?

A Hash Table is a high-efficiency data structure that stores key-value pairs.It uses a hash function to map keys to storage locations, achieving average O(1) time complexity for fast insertions, lookups, and deletions.The index functions as a storage location for the matching value. In simple words, it maps the keys with the value.Widely used in caching systems, database indexing, and compiler symbol tables.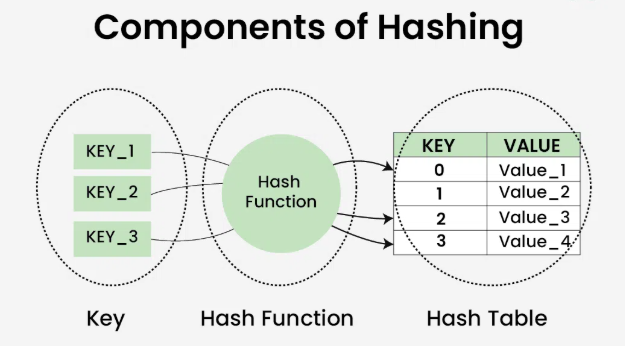

Core Concepts

Key: A unique identifier for the data.
Value: The data associated with the key (simplified to just storing keys in this example).
Bucket: A storage unit in the hash table (typically an array).
Hash Functions:
A hash function converts a key into an index for the underlying array:
- Deterministic: Same key always produces the same index.
- Efficient: Computed quickly to avoid performance bottlenecks.
- Uniform: Distributes keys evenly to minimize collisions.
Handling Hash Collisions:
When two different keys produce the same index, a collision occurs. Common solutions include:
- Seperate Chaining: Store conflicting elements in a linked list at the same index.
- Open Addressing: Find the next available slot in the array.

In addition to hash tables, arrays and linked lists can also be used to implement query functionality, but the time complexity is different.

	Array	Linked List	Hash Table
Search	O(n)	O(n)	O(1)
Insert	O(1)	O(1)	O(1)
Delete	O(n)	O(n)	O(1)

Per aboved comparison, the time complexity for operations (insertion, deletion, searching, and modification) in a hash table is O(1), which is highly efficient.

Common operations of hash table

Common operations of a hash table include: initialization, querying, adding key-value pairs, and deleting key-value pairs. Here is an example code:

/* Initialize hash table */
Dictionary<int, string> map = new() {
    /* Add operation */
    // Add key-value pair (key, value) to hash table
    { 13835, "Tom" },
    { 16937, "Jerry" },
    { 16852, "Steve" },
    { 13200, "James" },
    { 14583, "Lisa" }
};

/* Query operation */
// Input key into hash table, get value
string name = map[16937];

/* Delete operation */
// Delete key-value pair (key, value) from hash table
map.Remove(14583);

There are three common ways to traverse a hash table: traversing key-value pairs, traversing keys, and traversing values. Here is an example code:

/* Traverse hash table */
// Traverse key-value pairs Key->Value
foreach (var kv in map) {
    Console.WriteLine(kv.Key + " -> " + kv.Value);
}
// Traverse keys only
foreach (int key in map.Keys) {
    Console.WriteLine(key);
}
// Traverse values only
foreach (string val in map.Values) {
    Console.WriteLine(val);
}

Hash Collision

The hashing process generates a small number for a big key, so there is a possibility that two keys could produce the same value. The situation where the newly inserted key maps to an already occupied, and it must be handled using some collision handling technology.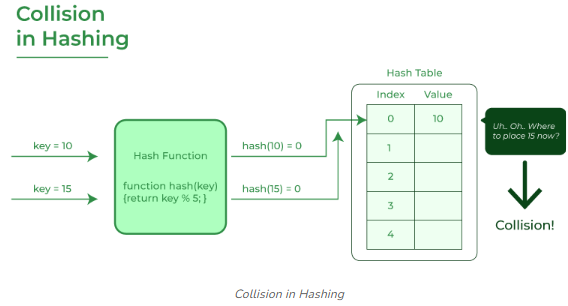

There are mainly two methods to handle collision:

Separate Chaining
Open Addressing

Separate Chaining

Separate chaining converts a single element into a linked list, treating key-value pairs as list nodes, storing all colliding key-value pairs in the same linked list.
The operations of a hash table implemented with separate chaining have changed as follows:

Searching Elements: Input key, obtain the bucket index through the hash function, then access the head node of the linked list. Traverse the linked list and compare key to find the target key-value pair.
Inserting Elements: Access the head node of the linked list via the hash function, then append the node (key-value pair) to the list.
Deleting Elements: Access the head of the linked list based on the result of the hash function, then traverse the linked list to find the target node and delete it.

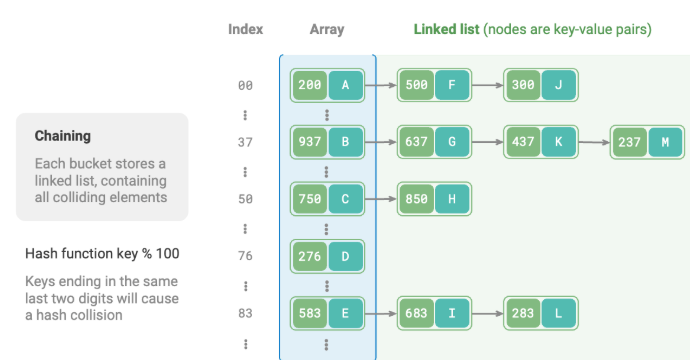
The code below provides a simple implementation of a separate chaining hash table, with two things to note:

Lists (dynamic arrays) are used instead of linked lists for simplicity. In this setup, the hash table (array) contains multiple buckets, each of which is a list.

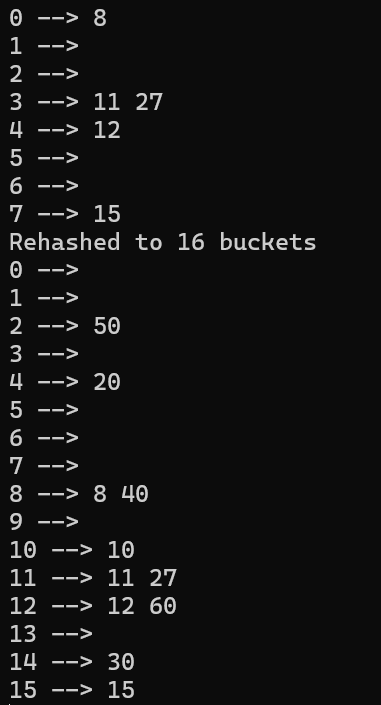
This implementation includes a hash table resizing method. When the load factor exceeds 0.7, we expand the hash table to twice its original size.

class Hash
{
      int BUCKET;
      List<int>[] table;
      int elementCount;
      const double LOAD_FACTOR_THRESHOLD = 0.7;
      public Hash(int V)
      {
          this.BUCKET = V;
          table = new List<int>[BUCKET];
          elementCount = 0;
          for (int i = 0; i < BUCKET; i++)
              table[i] = new List<int>();
      }
      // Hash function to map values to key
      private int hashFunction(int x)
      {
          int hash = x.GetHashCode();
          return (hash % BUCKET + BUCKET) % BUCKET;
      }
      double GetLoadFactor()
      {
          return (double)elementCount / BUCKET;
      }
      void Rehash()
      {
          int oldBucket = BUCKET; // old bucket
          int newBucket = oldBucket * 2; // new bucket
          List<int>[] newTable = new List<int>[newBucket];
          for(int i = 0; i < newBucket; i++)
          {
              newTable[i] = new List<int>();
          }

          for(int i = 0;i< oldBucket; i++)
          {
              foreach(int key in table[i])
              {
                  int newIndex = key%newBucket;

                  if (!newTable[newIndex].Contains(key))
                  {
                      newTable[newIndex].Add(key);
                  }
                  
              }
          }
          table = newTable;
          BUCKET = newBucket;
          Console.WriteLine($"Rehashed to {newBucket} buckets");
      }
      public bool Contains(int key)
      {
          int index = hashFunction(key);
          return table[index].Contains(key);
      }
      public void insertItem(int key)
      {
          if (Contains(key))
          {
              Console.WriteLine($"Key {key} already exists");
              return;
          }
          int index = hashFunction(key);
          table[index].Add(key);

          elementCount++;
          if(GetLoadFactor()> LOAD_FACTOR_THRESHOLD)
          {
              Rehash();
          }
      }
      // Deletes a key from the hash table
      public void deleteItem(int key)
      {
          int index = hashFunction(key);
          table[index].Remove(key);
          elementCount--;
      }
      public void displayHash()
      {
          for (int i = 0; i < BUCKET; i++)
          {
              Console.Write(i + " --> ");
              foreach (int x in table[i])
                  Console.Write(x + " ");
              Console.WriteLine();
          }
      }
}

It is worth noting that when the linked list is very long, the query efficiency
is poor. In this case, the list can be converted to an “AVL tree” or “Red-Black tree” to optimize the time complexity of the query operation to O(log n).

Open Addressing

In open addressing, all elements are stored in the hash table itself. Each table entry contains either a record or NIL. When searching for an element, we examine the table slots one by one until the desired element is found or it is clear that the element is not in the table.

Probe Strategies:

Linear Probing:
In linear probing, the hash table is searched sequentially that starts from the original location of the hash. If in case the location that we get is already occupied, then we check for the next location.
Quadratic Probing: Search with step size i^2.
Double Hashing: Use a second hash function to calculate the step size.

class OpenAddressingHash {
    private int BUCKET;             // Number of buckets
    private int?[] table;           // Storage for keys, null indicates empty

    public OpenAddressingHash(int V) {
        this.BUCKET = V;
        table = new int?[BUCKET]; // Initialize as empty
    }

    // Hash function: Modulo operation
    private int hashFunction(int x) {
        return (x % BUCKET);
    }

    // Insert item
    public bool insertItem(int key) {
        if (isFull()) return false; // Hash table is full

        int index = hashFunction(key);

        // Linear probing
        int i = 0;
        while (table[(index + i) % BUCKET] != null) {
            i++;
        }

        table[(index + i) % BUCKET] = key;
        return true;
    }

    // Search item
    public bool searchItem(int key) {
        int index = hashFunction(key);

        int i = 0;
        while (table[(index + i) % BUCKET] != null) {
            if (table[(index + i) % BUCKET] == key)
                return true;
            i++;
        }

        return false;
    }

    // Delete item
    public bool deleteItem(int key) {
        int index = hashFunction(key);

        int i = 0;
        while (table[(index + i) % BUCKET] != null) {
            if (table[(index + i) % BUCKET] == key) {
                table[(index + i) % BUCKET] = null; // Mark as empty
                return true;
            }
            i++;
        }

        return false;
    }

    // Check if hash table is full
    private bool isFull() {
        foreach (var item in table) {
            if (item == null)
                return false;
        }
        return true;
    }

    // Display hash table
    public void displayHash() {
        for (int i = 0; i < BUCKET; i++) {
            Console.WriteLine($"{i} --> {table[i]}");
        }
    }
}

Hash Alogrithm

Goals of hash algorithms

To achieve a fast and stable hash table data structure, hash algorithms should have the following characteristics:

Determinism: For the same input, the hash algorithm should always produce the same output. Only then can the hash table be reliable.
High efficiency: The process of computing the hash value should be fast enough. The smaller the computational overhead, the more practical the hash table.
Uniform distribution: The hash algorithm should ensure that key-value pairs are evenly distributed in the hash table. The more uniform the distribution, the lower the probability of hash collisions.

Your company might use a hashing algorithm for:

Password storage. You must keep records of all of the username/password combinations people use to access your resources. But if a hacker gains entry, stealing unprotected data is easy. Hashing ensures that the data is stored in a scrambled state, so it is harder to steal.
Digital signatures. A tiny bit of data proves that a note wasn’t modified from the time it leaves a user’s outbox and reaches your inbox.
Document management. Hashing algorithms can be used to authenticate data. The writer uses a hash to secure the document when it’s complete. The hash works a bit like a seal of approval.
A recipient can generate a hash and compare it to the original. If the two are equal, the data is considered genuine. If they don’t match, the document has been changed.

Common hash algorithms

Over the past century, hash algorithms have been in a continuous process of upgrading and optimization. Some researchers strive to improve the performance of hash algorithms, while others, including hackers, are dedicated to finding security issues in hash algorithms.

MD5 and SHA-1 have been successfully attacked multiple times and are thus abandoned in various security applications.
SHA-2 series, especially SHA-256, is one of the most secure hash algorithms to date, with no successful attacks reported, hence commonly used in various security applications and protocols.
SHA-3 has lower implementation costs and higher computational efficiency compared to SHA-2, but its current usage coverage is not as extensive as the SHA-2 series.

	MD5	SHA-1	SHA-2	SHA-3
Release Year	1992	1995	2002	2008
Output Length	O(1)	O(1)	O(1)	224/256/384/512 bit
Hash Collisions	Frequent	Frequent	Rare	Rare
Security Level	Low, has been successfully attacked	Low, has been successfully attacked	High	High
Applications	Abandoned, still used for data integrity checks	Abandoned	Cryptocurrency transaction verification, digital signatures, etc.	Can be used to replace SHA-2

Four Sum

Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:

0 <= i, j, k, l < n

nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

public int FourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
       Dictionary<int, int> dic = new Dictionary<int, int>();
        foreach(var i in nums1){
            foreach(var j in nums2){
                int sum = i + j;
                if(dic.ContainsKey(sum)){
                    dic[sum]++;
                }else{
                    dic.Add(sum, 1);
                }
                
            }
        }
        int res = 0;
         foreach(var a in nums3){
            foreach(var b in nums4){
                int sum = a+b;
                if(dic.TryGetValue(-sum, out var result)){
                    res += result;
                }
            }
        }
        return res;
}